1. Which of the following best describes the primary function of a geodetic datum?
A) A model for predicting economic trends.
B) A framework for measuring Earth’s positions.
C) A method for determining climate change impacts.
D) A system for mapping urban development.
B) A framework for measuring Earth’s positions.
2. In the context of geodetic datums, what is the role of the Prime Meridian?
A) Specifies the Earth’s center point.
B) Determines global time zones.
C) Defines the longitudinal reference line.
D) Measures Earth’s gravitational field
C) Defines the longitudinal reference line.
3. Why are different geodetic datums used by various countries and regions?
A) To enhance political boundary discussions.
B) To simplify global navigation systems.
C) To fit the curvature of Earth’s surface locally.
D) To comply with international trade laws.
C) To fit the curvature of Earth’s surface locally.
4. How do geodetic datums assist in property valuation models?
A) Through automated sales prediction algorithms.
B) Via historical analysis of ownership transfers.
C) By offering detailed climate data for properties.
D) They assess proximity to geographic features affecting value.
D) They assess proximity to geographic features affecting value.
5. What is the significance of geodetic datums in land use planning?
A) Predicting population growth in rural areas.
B) Managing financial investment portfolios.
C) Assessing suitability for various developmental purposes.
D) Enhancing biodiversity conservation efforts.
C) Assessing suitability for various developmental purposes.
6. Which characteristic uniquely identifies a coordinate system in geometry?
A) The requirement for coordinates to always be real numbers.
B) The exclusive use of orthogonal coordinate axes.
C) The inclusion of homogeneous coordinates in all systems.
D) The ability to translate geometric problems into numerical problems.
D) The ability to translate geometric problems into numerical problems.
7. How are cylindrical and spherical coordinate systems related to the polar coordinate system?
A) Cylindrical replaces r with a z-coordinate, spherical uses r, φ, θ.
B) Cylindrical adds a z-coordinate, and spherical uses polar coordinates (ρ, φ) for (r, z).
C) Both convert polar coordinates into Cartesian systems directly.
D) The systems are independent and don’t build on polar coordinates.
B) Cylindrical adds a z-coordinate, and spherical uses polar coordinates (ρ, φ) for (r, z).
8. What is a fundamental difference between coordinate lines and coordinate curves in coordinate systems?
A) Coordinate lines in Cartesian systems are straight, while curves can be any shape.
B) Coordinate lines only appear in polar coordinates, curves in Cartesian.
C) Coordinate lines are always circles, while curves are parabolas.
D) Both terms are interchangeable and refer to straight lines.
A) Coordinate lines in Cartesian systems are straight, while curves can be any shape.
9. What role do coordinate maps play in the theory of manifolds?
A) They convert three-dimensional spaces into two-dimensional ones.
B) They only relate to topological boundaries, not coordinate systems.
C) They provide a coordinate system for subsets, ensuring each point has one set of coordinates.
D) They define non-Euclidean spaces as Euclidean.
C) They provide a coordinate system for subsets, ensuring each point has one set of coordinates.
10. In transformative coordinate systems, what defines the distinction between active and passive transformations?
A) Active changes the object’s coordinates, passive changes the observer’s coordinate frame.
B) The active allows numerical conversion; passive allows rotation.
C) Active transforms affect color and shape, passive affect location only.
D) Active is fixed to original points; passive duplicates them.
A) Active changes the object’s coordinates, passive changes the observer’s coordinate frame.
11. Which description accurately summarizes the role of a coordinate transformation in relation to different coordinate systems?
A) Coordinate transformations identify the number of coordinates needed for each system.
B) Coordinate transformations introduce new dimensions to existing coordinate systems.
C) Coordinate transformations provide formulas to convert coordinates between different systems.
D) Coordinate transformations change the geometric interpretation of figures.
C) Coordinate transformations provide formulas to convert coordinates between different systems.
12. What is a defining feature of the Cartesian coordinate system when generalized to n-dimensional Euclidean space?
A) Coordinates are the intersections of curves in the space.
B) Coordinates are derived from the rotational transformation between axes.
C) Coordinates are defined by signed distances to n mutually orthogonal planes.
D) Coordinates vary continuously producing non-linear surfaces.
C) Coordinates are defined by signed distances to n mutually orthogonal planes.
13. How does the polar coordinate system differ from the Cartesian coordinate system in representing points on a plane?
A) Polar coordinates convert angular measurements to linear distances.
B) Polar coordinates depict points with perpendicular bisectors.
C) Polar coordinates use angles and signed distances from a pole, unlike Cartesian’s perpendicular lines.
D) Polar coordinates determine positions using vertical and horizontal lines.
C) Polar coordinates use angles and signed distances from a pole, unlike Cartesian’s perpendicular lines.
14. What characteristic feature defines a homogeneous coordinate system in the plane?
A) Homogeneous coordinates rely on the ratios of coordinates, not their absolute values.
B) Homogeneous coordinates utilize the angle and arc length to specify positions.
C) Homogeneous coordinates adjust for non-linear transformations of space.
D) Homogeneous coordinates are defined by the absolute distances from a fixed point.
A) Homogeneous coordinates rely on the ratios of coordinates, not their absolute values.
15. What is a necessary attribute for a manifold to be considered differentiable?
A) Aligned coordinate maps must transition smoothly via differentiable functions.
B) All coordinate maps must convert to polar systems.
C) Coordinate maps must be uniformly orthogonal.
D) Coordinate maps should exhibit non-consistent overlaps.
A) Aligned coordinate maps must transition smoothly via differentiable functions.
16. What is the first step in changing from one map projection to another, as described in the context?
A) Calculate the scale factor and apply it to both coordinate systems.
B) Use forward equation of target projection to get new Cartesian coordinates.
C) Directly apply transformation parameters from source to target projection.
D) Use inverse equation of source projection to get geographic coordinates.
D) Use inverse equation of source projection to get geographic coordinates.
17. Which transformation method is specifically noted for its non-reversibility in the text?
A) The Abridged Molodensky transformation.
B) The geocentric translation method.
C) The Helmert 7-parameter transformation.
D) The Molodensky-Badekas 10-parameter transformation.
D) The Molodensky-Badekas 10-parameter transformation.
18. What is required for a 2D Cartesian transformation when the input coordinate system is unknown?
A) Exact height coordinates in both systems.
B) A detailed Digital Elevation Model of the area.
C) 2D ground control points or common points.
D) Both projected and geographic coordinate systems.
C) 2D ground control points or common points.
19. Why might 2D Cartesian transformations offer better accuracy than projection equations over small areas?
A) They apply universal parameters irrespective of map scale.
B) They incorporate a standard scale factor in transformations.
C) They handle coplanar control points well, if the area isn’t too large.
D) They inherently correct for Earth’s curvature in all calculations.
C) They handle coplanar control points well, if the area isn’t too large.
20. What is a primary reason for needing datum transformations in mapping practices?
A) To simplify the data collected from different geocentric systems.
B) To ensure all map data is transformed into a global Cartesian system.
C) To convert satellite data exclusively into the WGS84 datum.
D) To achieve a perfect match between adjacent maps with different underlying datums.
D) To achieve a perfect match between adjacent maps with different underlying datums.
21. Which method describes a transformation using three rotation angles, an origin shift, and a scale factor?
A) The Molodensky-Badekas 10-parameter transformation.
B) The affine transformation.
C) The Helmert 7-parameter transformation.
D) The geocentric translation.
C) The Helmert 7-parameter transformation.
22. What is required to conduct a 2D Cartesian transformation when the coordinate system is unknown?
A) The scale parameters and rotation axes.
B) Only the geographic coordinates of the input data.
C) 2D ground control points or common points.
D) Simply the source’s ellipsoidal height.
C) 2D ground control points or common points.
23. Which transformation is considered reversible, maintaining parameter integrity for reverse calculations?
A) Conformal transformation.
B) Geographic offset method.
C) Molodensky-Badekas 10-parameter transformation.
D) Helmert 7-parameter transformation.
D) Helmert 7-parameter transformation.
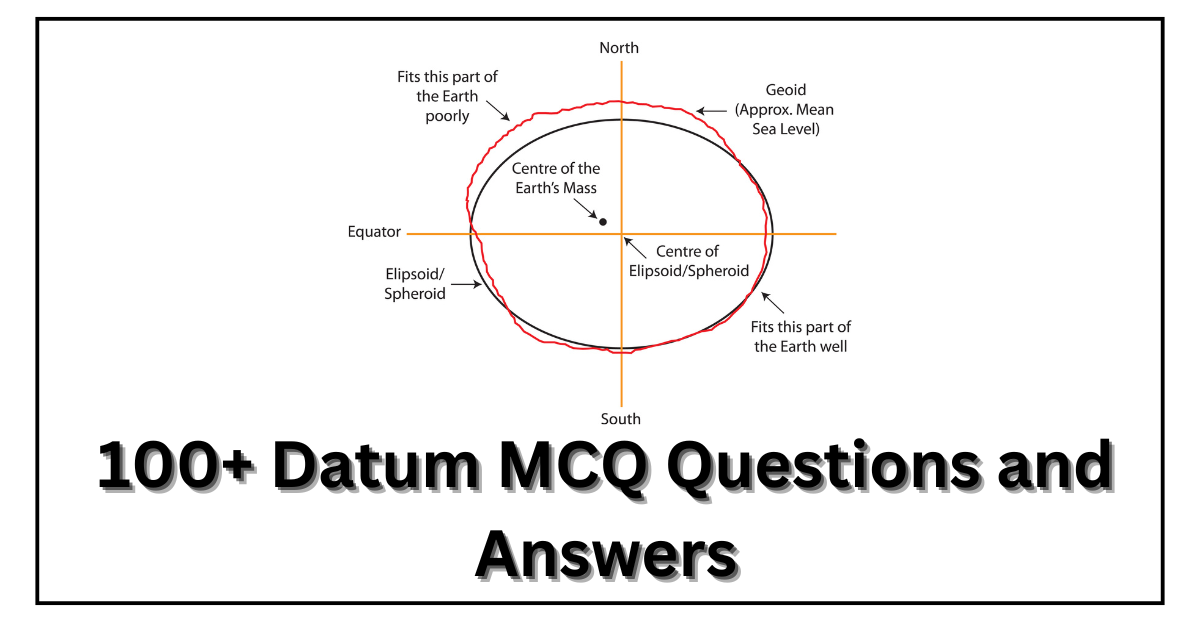
24. Which type of latitude is primarily implied in general usage and is based on an imaginary plane passing through Earth’s center?
A) Geographic latitude
B) Geocentric latitude
C) Celestial latitude
D) Astronomical latitude
B) Geocentric latitude
25. How does astronomical latitude differ from geocentric latitude in terms of the points it considers?
A) It’s determined by the tilt of Earth’s axis.
B) It is measured only at the Equator.
C) It considers the direction of gravity at a given location.
D) It focuses strictly on solar positions.
C) It considers the direction of gravity at a given location.
26. What is the derived method for calculating geographic latitude that involves measuring celestial bodies?
A) Using a sextant to measure the Sun’s angle at noon
B) Taking temperature gradients along the equator
C) Measuring seismic wave patterns
D) Calculating the angle by observing tidal shifts
A) Using a sextant to measure the Sun’s angle at noon
27. What is the reason for the variation in the length of one degree of latitude from 110.567 km at the equator to 111.699 km at the poles?
A) Magnetic declination varies
B) Seasonal temperature changes
C) Earth’s curvature is not uniform.
D) Ocean currents cause shifts
C) Earth’s curvature is not uniform.
28. Why does the distance per degree of longitude significantly change from the Equator to the poles?
A) Varying solar radiation levels
B) Pressure changes in atmospheric layers
C) Lines of longitude are not parallel, narrowing towards the poles.
D) Tectonic activity shifts surface lines
C) Lines of longitude are not parallel, narrowing towards the poles.
29. What is the primary purpose of a rotation matrix in three-dimensional space?
A) To translate coordinates from one plane to another
B) To change the orientation of a vector while preserving distances
C) To scale vectors in proportional dimensions
D) To change the vector’s magnitude while keeping direction
B) To change the orientation of a vector while preserving distances
30. What matrix product results from first rotating about the z-axis by θ and then about the x-axis by α?
A) Rz(α)⋅Rx(θ)
B) Rx(α)⋅Rz(θ)
C) Ry(α)⋅Rz(θ)
D) Ry(θ)⋅Rx(α)
B) Rx(α)⋅Rz(θ)
31. How does a reflection matrix differ from a rotation matrix in their applications?
A) It mirrors points across a specified plane instead of rotating them
B) It changes the color of points after transformation
C) It scales points proportionally across all axes
D) It rotates points while applying an equal translation
A) It mirrors points across a specified plane instead of rotating them
32. Which axis rotation matrix includes the elements cos(α), -sin(α), sin(α), and cos(α) arranged in a particular order?
A) Rotation about the y-axis
B) Rotation about the z-axis
C) Reflection across the XY-plane
D) Rotation about the x-axis
D) Rotation about the x-axis
33. In GNSS applications, why are rotation matrices important?
A) To convert satellite data into usable positional information
B) To isolate specific frequencies from satellite signals
C) To create synthetic satellite trajectories
D) To encrypt positional data for secure transmission
A) To convert satellite data into usable positional information
34. Which axis in the Earth-Centered, Earth-Fixed (ECEF) coordinate system points toward the intersection of the Equator and the Prime Meridian?
A) The axis toward 90° East longitude
B) The z-axis
C) The y-axis
D) The x-axis
D) The x-axis
35. How are geographic coordinates primarily expressed when representing a point on the Earth’s surface?
A) Through vector magnitudes
B) As ECEF coordinates
C) In terms of latitude and longitude
D) Using Cartesian coordinates
C) In terms of latitude and longitude
36. What key component of the geographic coordinate system is defined as the angle between a point and the Equator?
A) Azimuth
B) Longitude
C) Altitude
D) Latitude
D) Latitude
37. What is necessary for transforming geographic coordinates to ECEF geocentric coordinates?
A) Direct extrapolation from geographic grids
B) Formulas involving latitude, longitude, and altitude
C) Simple linear mapping techniques
D) Basic trigonometric calculations without altitude consideration
B) Formulas involving latitude, longitude, and altitude
38. Which application relies on geocentric coordinates for accurate modeling of Earth’s shape and understanding its gravitational field?
A) Surveying
B) Land Delineation
C) Geospatial Analysis
D) Earth Dynamics
D) Earth Dynamics
39. What are the key components required for completing a local to global coordinate transformation in geodesy?
A) Choosing projection methods, applying geocentric models, and Helmert transformation.
B) Determining angles, calculating distances, and overlaying coordinates.
C) Identifying reference frames, using transformation parameters, and mathematical transformation.
D) Selecting datum, executing affine transformation, and using GPS.
C) Identifying reference frames, using transformation parameters, and mathematical transformation.
40. How does the Helmert transformation differ from the affine transformation?
A) The Helmert transformation maintains angles and distances.
B) The Helmert transformation alters the datum parameters.
C) The Helmert transformation is limited to two-dimensional transformations.
D) The Helmert transformation includes nonlinear equations.
A) The Helmert transformation maintains angles and distances.
41. Why is the validation step critical after implementing the local to global transformation?
A) To assess the accuracy of the transformed coordinates against control points.
B) To determine the number of control points needed for the survey.
C) To select the correct geodetic datum for the transformation process.
D) To calculate the scale of the transformation network.
A) To assess the accuracy of the transformed coordinates against control points.
42. Which method is commonly used to address datum discrepancies and enhance transformation accuracy in geodesy?
A) Geodetic datum transformations tailored for specific procedures.
B) Utilizing statistical data models for prediction analysis.
C) Applying geometric corrections to local systems.
D) Conducting repeated surveys for data alignment.
A) Geodetic datum transformations tailored for specific procedures.
43. What major challenge can arise from differences in local coordinate systems during global transformations?
A) Complex geometric relationships due to Earth’s curvature and local variability.
B) Limited satellite coverage in remote regions.
C) Excessive computational resources for small areas.
D) Overlapping geospatial data between rival systems.
A) Complex geometric relationships due to Earth’s curvature and local variability.
1 thought on “100+ Datum MCQ Questions and Answers”